Fractals zitten vol tegenstrijdigheden: enerzijds doodsimpel, anderzijds supercomplex; enerzijds oeroud (ze bestaan in de natuur), anderzijds splinternieuw (ze werden pas ernstig bestudeerd einde 20ste eeuw).
De term 'fractal' is afgeleid van het Latijnse woord fractus (gebroken) en werd in 1975 voor het eerst gebruikt door de Franse wiskundige Benoit Mandelbrot.
Een fractal kan het best omschreven worden als een complexe wiskundige figuur met een zeer simpele basis: hij heeft een eenvoudige formule en 3 bijzondere karakteristieke eigenschappen.

Zelfgelijkvormigheid: het object is exact of bij benadering gelijkvormig aan een deel van zichzelf. De onderdelen van de figuur hebben dus (ongeveer) dezelfde vorm als de figuur zelf, maar dan op kleinere schaal.

Fractale dimensie: een verhouding die vergelijkt in welke mate een detail in een patroon verandert met de schaal waarop dit patroon wordt gemeten.

Iteratie: een in principe oneindige herhaling. Dit betekent dat de fractal zichzelf zal herhalen als je er verder op inzoomt.

In de natuur vinden we heel wat fractals: bekijk eens een sneeuwkristal met een steeds sterkere uitvergroting, het sneeuwkristal blijft steeds dezelfde zeshoekige symmetrie vertonen.
Ook in een varen kan je een fractal herkennen: een varenblad bestaat uit blaadjes van dezelfde vorm (de afbeelding hiernaast is geen echte varen, maar een op computer getekende fractal).
De eerste studies ontstonden reeds voor het woord fractal bestond: begin 20ste eeuw bestudeerde de Engelse wiskundige Lewis Fry Richardson de lengte van de Engelse kust en kwam hij tot het besluit dat de lengte van de kustlijn afhankelijk was van de lengte van het gebruikte meettoestel.
Met een extraklein meettoestel zouden we dus een extralange kustlijn hebben.
Dit principe steunt op de Koch-kromme, die de gelijknamige Zweedse wiskundige enkele jaren voordien ontdekte.

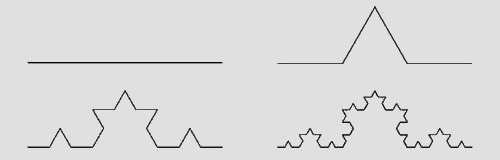
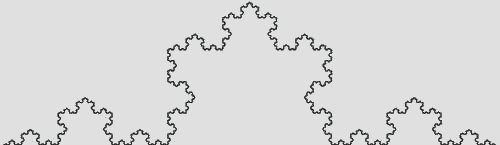
Enkele jaren later ontdekte de Poolkse wiskundige Waclaw Sierpinski de driehoek van Sierpinski.
In een gelijkzijdige driehoek wordt de driehoek, gevormd door de middens van de drie zijden, verwijderd. Vervolgens wordt deze procedure herhaald in elk van de drie overgebleven driehoeken. Deze procedure wordt nu oneindig herhaald.
De Spons van Menger werd in 1926 beschreven door de Oostenrijkse wiskundige Karl Menger.
Men verkrijgt deze spons door een vierkant op te splitsen in negen congruente vierkanten. Vervolgens laat men het middelste vierkant weg, zodat er nog acht vierkantjes overblijven. Nu doet men weer hetzelfde bij deze acht vierkantjes, en nog eens, en nog eens, en nog eens, …
In 1942 bedacht de Nederlandse wiskundeleraar Albert E. Bosman de boom van Pythagoras.
De bouw van de boom van Pythagoras begint met een vierkant.
Bij de basisfiguur tekenen we een gelijkbenige rechthoekige driehoek op de bovenste vierkantszijde, met de vierkantszijde als schuine zijde van de driehoek (Pythagoras ken je nog wel).
Op de gelijkbenige rechthoekszijden van onze driehoek tekenen we terug een vierkant.
Op elk der twee kleinere identieke vierkantjes passen we terug dezelfde bewerking toe, en nog eens, en nog eens, ...
Er bestaan heel wat variaties op deze basisfiguur: andere hoeken, lijnen die splitsen, enz.
Zo starten we in het laatste model alweer met een vierkant.
Op de bovenste zijde van het vierkant construeren we nu een niet gelijkbenige rechthoekige driehoek met de de vierkantszijde als schijne zijde van de driehoek.
Op de andere zijdes van onze driehoek construeren we terug een vierkant.
Op de bovenste zijde van de niet identieke vierkanten construeren we alweer een niet gelijkbenige rechthoekige driehoek met de de vierkantszijde als schijne zijde van de driehoek, enz.
Bij alweer een andere variante construeren we een gelijkzijdige driehoek op de vierkantszijde.
Zoals je ziet, zijn de mogelijkheden bij de boom van Pythagoras oneindig.

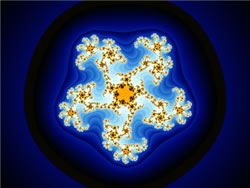
Grote bekendheid verwierven de fractals echter pas op het einde van de 20ste eeuw, als de Franse wiskundige Benoit Mandelbrot op zijn computer de Mandelbrotverzamelingen grafisch voorstelde.


Eerst toch even een waarschuwing: hier zullen we ons wat intenser moeten bezighouden met de wiskunde.
De Mandelbrotverzameling is een verzameling van complexe getallen.
Een complex getal bestaat uit twee delen: een reëel getal en een imaginair getal.
Reële getallen zijn de "gewone" getallen (kommagetallen en negatieve getallen inbegrepen).
Imaginaire getallen steunen op de imaginaire eenheid i. Nu is i dusdanig gedefinieerd dat i² = - 1, of anders gezegd: i is gelijk aan de wortel van -1.
Een voorbeeld van een complex getal is 2 + 0.5i. In dit getal is 2 het reële deel en 0.5i het imaginaire deel.
Nu kunnen we complexe getallen weergeven als punten in het complexe vlak, waarbij het reële deel op de horizontale as (x-as) en het imaginaire deel op de verticale as (y-as) staat.
Het complexe getal 2 + 0.5i heeft dus in het complexe vlak de coördinaten (2 , 0.5).
De Mandelbrotverzameling ontstaat nu door herhaaldelijk een bepaalde wiskundige bewerking uit te voeren op een verzameling complexe getallen.
De basisbewerking is Z → Z ² + C: we kwadrateren een complex getal en tellen er dan het oorspronkelijke complex getal bij op.
Voorbeeld: we nemen het complexe getal C = 2 + 0.5i.
De coördinaten van ons eerste punt zijn dus (2, 0.5).
We kwadateren dit: (2 + 0.5i)² = 2² + 2 * 0.5i + 2 * 0.5i + 0.5² * i², na vereenvoudiging: 4 + 2i + 0.25 * i²
Gezien i² = -1, geeft dit dus: 4 + 2i - 0.25 of 3.75 + 2i.
Vervolgens wordt hier het oorspronkelijke getal bij opgeteld: 3.75 + 2i + 2 + 0.5i = 5.75 + 2.5i.

De coördinaten van ons volgend punt zijn dus: (5.75, 2.5).
De bewerkingen worden erhaald op de nieuwe coördinaten: kwadrateren en daarna het oorspronkelijke getal er bij optellen.
Wanneer we deze bewerkingen voortdurend herhalen voor alle complexe getallen, blijken er twee soorten complexe getallen te zijn.
De eerste soort levert tijdens deze bewerking een losse sequentie op: de uitkomsten worden steeds groter naarmate de bewerking vaker herhaald wordt. Dit is onder meer het geval bij het voorbeeld met het getal 2 + 0.5i.
Andere complexe getallen leveren echter een vaste sequentie op: hoe vaak de bewerking ook herhaald wordt, de uitkomsten blijven altijd binnen bepaalde waarden.
Een voorbeeld: het getal -2 + 0i, of simpelweg -2. Het kwadraat van -2 is 4, optellen van -2 levert vervolgens 2 op. Herhalen van de bewerking (kwadraat van 2, daarna het oorspronkelijke getal -2 erbij optellen) levert telkens opnieuw 2 op.
De Mandelbrotverzameling bestaat nu uit alle getallen die een vaste sequentie blijken op te leveren.
De getallen die leiden tot een losse sequentie vallen buiten de Mandelbrotverzameling.
De vaste sequenties blijven dus binnen bepaalde waarden en als we deze waarden weergegeven in het complexe vlak, vormen zij een cirkel.
In afbeeldingen wordt de Mandelbrotverzameling meestal met een zwarte kleur weergegeven en de getallen die buiten de verzameling vallen met een andere kleur.
Vaak wordt een groot aantal kleuren gebruikt die geleidelijk in elkaar overgaan.
De kleuren zijn afhankelijk van het aantal iteraties dat nodig was vooraleer de losse sequentie een waarde oplevert die buiten de Mandelbrotverzameling valt.
In functie van de waarde die we kiezen voor ons complex getal en de gebruikte bewerking, krijgen we verschillende resultaten.
Door in te zoomen op een deel van de figuur krijgen we nieuwe figuren. Blijven we steeds verder inzoomen, dan komen we uiteindelijk terug bij onze oorspronkelijke figuur.
Tegenwoordig zijn er heel wat toepassingen van fractals:
- Elk computerspel maakt gebruik van fractals om de onregelmatige structuren van wolken en bergen na te bootsen.
- Fractals worden gebruikt in modellen voor weerpatronen en klimatologische veranderingen.
- Astronomische verschijnselen, zoals de vorming van quasars en sterrenstelsels, laten zich uitstekend simuleren door middel van fractals.
Heb je de smaak te pakken? Op het web kan je diverse gratis programma’s vinden om zelf fractals te genereren op je computer.
Hieronder zie je enkele Mandelbrot-fractals.
Meer voorbeelden van fractals kan je vinden onder het menu Pictures/Fractals.